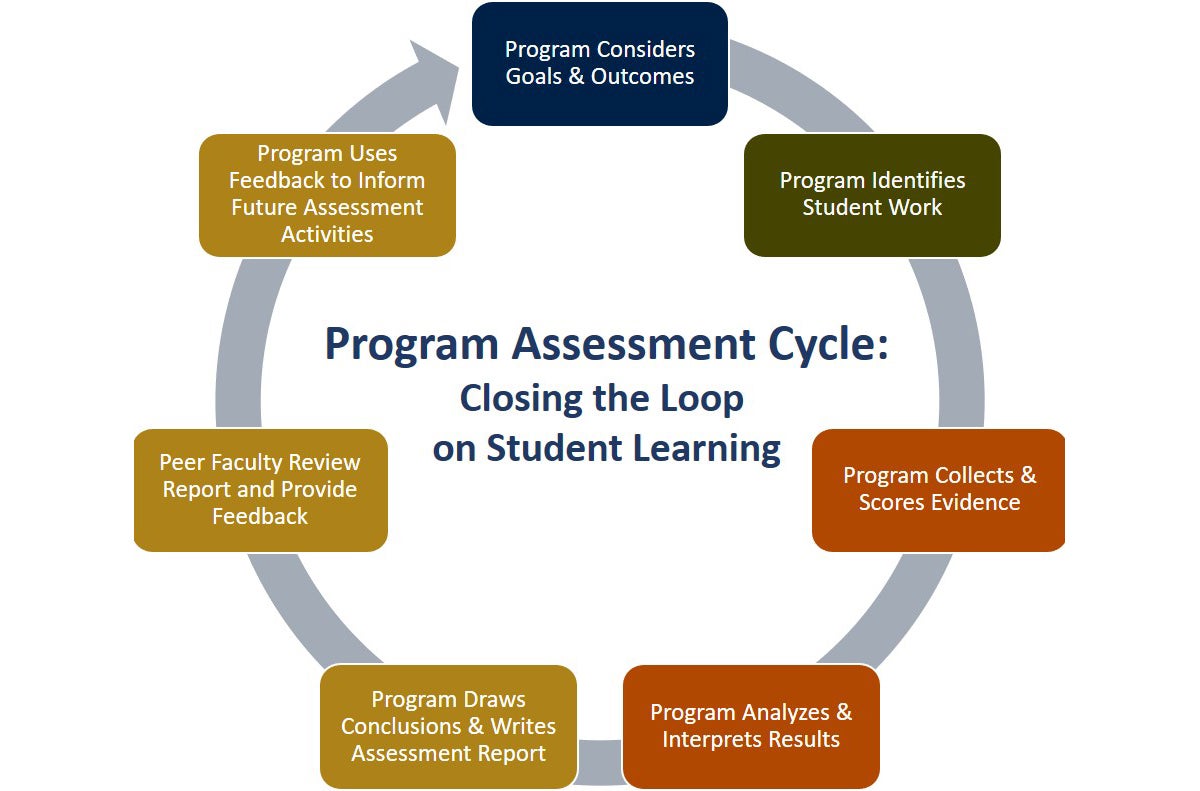
At the University of Rhode Island, assessment at the program level refers to the collection, review, and use of information about student learning for the purpose of continual improvement by monitoring the impact of the curriculum on student success. This information supports a climate of learning improvement by influencing teaching practices, policies and ultimately, the conditions that will improve student learning. Assessment for learning is a faculty-owned process, driven by thoughtful questions about learning, with clear and measurable expectations about what graduates of a program should know and be able to do.
Program-level assessment is an integral part of URI’s commitment to evidence-informed reflection and continual improvement and is aligned with expectations from the University’s accrediting body, the New England Commission of Higher Education.
The Assessment team supports all phases of the assessment process, providing templates, resources, and consultation services. Contact us: assess@uri.edu
Consultations
The ATL team holds a wide range of experience and knowledge to help you meet your teaching and learning goals, regardless of modality, level of experience teaching, or discipline.
Book a Consultation